主流Nerf质量优化和计算加速方法学习——体渲染、体素、位置编码

• 体渲染：渲染粒子云
• 体素渲染：Minecraft

(NIPS'20) Neural sparse voxel fields

• 场景划分为体素，每个体素8个顶点分配8个Embedding，体素内的任意点的Embedding由8个顶点Embedding插值得到，渲染任意点时合并8个Embedding作为MLP(Multi-layer Perceptron Network)输入，输出该点的颜色和占据概率
• 何谓之“稀疏”：训练时不包含场景信息的稀疏体素将被修剪

原理

对于体素集合$V=\{V_1,\dots,V_K\}$中的每个体素$V_i$，都定义一个函数$F_\theta^i$，其以体素中的点$\bm p\in V_i$为输入，输出颜色$\bm c$和概率密度$\sigma$：

$\begin{aligned} F_\theta^i&:(\bm g_i(\bm p), \bm v)\rightarrow(\bm c,\sigma)&\forall\bm p\in V_i\\ g_i(\bm p)&=\zeta(\chi(\tilde{g_i}(\bm p_1^*),\dots,\tilde{g_i}(\bm p_8^*)))\\ \mathcal V&=\{V_1,\dots,V_K\} \end{aligned}$

其中，$g_i(\bm p)$表示其对输入的坐标进行了一些处理，具体是：

1. 将体素的顶点上存储的嵌入向量进行插值得到体素内坐标点$\bm p$处的嵌入向量：$\chi$表示插值函数，$\bm p_1^*,\dots,\bm p_8^*$表示体素$V_i$的8个顶点，$\tilde{g_i}(\bm p_i^*)$表示这8个顶点对应的嵌入向量（注意这里公式不严谨，不同的点$\bm p$插值出来的嵌入向量应该是不一样的，公式中没有体现）；
2. 位置编码：$\zeta$是位置编码，即对插值得到的坐标点$\bm p$处的嵌入向量进行位置编码；
3. DNN推断：位置编码后的$\bm p$点特征向量和光线方向一起输入到$F_\theta^i$中推断，输出输出颜色$\bm c$和概率密度$\sigma$。

Nerf是NSVF的特殊情况

坐标不转化成嵌入直接位置编码后输入的话：

$\chi(\tilde{g_i}(\bm p_1^*),\dots,\tilde{g_i}(\bm p_8^*))=\bm p$

$F_\theta^i$就变成：

$F_\theta^i:(\zeta(\bm p), \bm v)\rightarrow(\bm c,\sigma)$

就是Nerf里的DNN推断。

所以Nerf就是没有坐标嵌入的特殊情况。 反过来讲，NSVF就是把Nerf里的输入点改成输入基于体素计算出的嵌入向量，这些嵌入向量在训练中可以预先存入一些信息，从而使得输入到DNN里的信息更多。 此外，稀疏体素给NSVF带来的性能提升也可以在Nerf上实现，只要想办法把三维区域用体素包起来就能实现一样的稀疏体素ray marching了。

体素存储颜色信息的渲染方案是NSVF的特殊情况

显然，如果$\tilde{g_i}(\bm p_i^*)$输出就是颜色：

$\tilde{g_i}(\bm p_i^*):\tilde{g_i}(\bm p)\rightarrow(\bm c,\sigma)$

并令$F_\theta^i$、$\zeta$、$\chi$都把输入做输出，那相当于就是每个体素存储一些颜色信息的方案（从不同方向看去颜色相同的点以体素为单位分别存储）。

Lombardi S, Simon T, Saragih J, et al. Neural volumes: Learning dynamic renderable volumes from images[J]. arXiv preprint arXiv:1906.07751, 2019.

估计透明度

本文定义的透明度为：

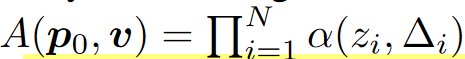
其中$(\bm p_0, \bm v)$是在用起点和方向表示一条光线，$A(\bm p_0, \bm v)$是这条光线上所有的采样点$\bm p$积累的透明度。结合上文写的体渲染公式：

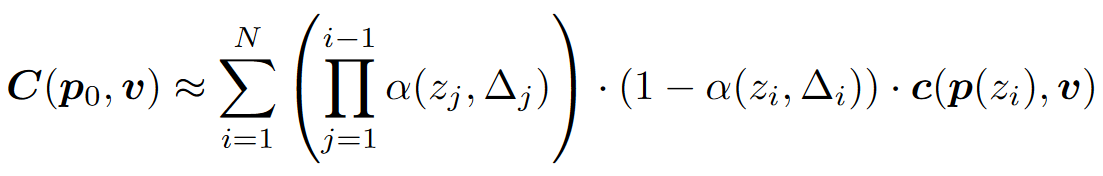
可以看出这个透明度实际上就是：

$A(\bm p_0, \bm v)=e^{-\sum_{k=1}^{N}\sigma_k \delta_k}$

其实就是Nerf体渲染公式里背景光项$I_0T_{N+1}$中的$T_{N+1}$。回忆学习体渲染时对背景光项的理解，$T_{N+1}$来自于透射比，其值越小表示背景光中透过的光强越低。

渲染流程

1. 计算各条光线起点和方向
2. 体素交叉判断：AABB test找出每条光线与体素交叉的位置
3. 体素内采样：在与体素交叉的位置内部进行采样，得到待计算的各$\bm p$点
4. DNN推断：将采样出的各$\bm p$点按上述公式转为嵌入向量后输入DNN，得到$(\bm c,\sigma)$
5. 提前退出：借鉴“表面”的思想，当光线上积累的透明度$A(\bm p_0, \bm v)$跌至阈值$\epsilon$以下时，视为物体内部，立即停止计算
6. 体渲染：之后的操作同Nerf里的体渲染

背景光项里的透射比->用作透明度估计->判定物体表面->用于计算优化，这真是个天才的想法。 顺着光线的方向采样，当背景光无法透过的时候不就说明物体此时已经不透明了吗！ 这简直是算法优化对物理过程的完美利用。 Nerf中的体渲染公式是没有体现背景光项的，作者一定对体渲染的公式有一个非常深刻的理解，并且知道Nerf里那个体渲染公式的推导过程，才能知道公式里实际上是忽略了这一项的。 作者把这一项找回来了不说，还顺着其的物理含义找到了一种能极大优化计算速度的方法。 很久没有体验这种茅塞顿开的感觉了。 佩服！

优势

因为体素是稀疏的，而且渲染时已知只有体素内有东西，所以只需要在光线与体素交叉的地方采样；并且还通过透明度$A(\bm p_0, \bm v)$估计和积累把采样控制在物体表面，所以：

1. 不需要像Nerf那样对光线上的所有点采样计算，极大节约计算成本；
2. 在体素内可以采样密度很高，有效提升计算精度。

总而言之，在重点区域提升采样密度，极大提高效率。 不过仔细想想这些东西其实也可以无缝迁移到Nerf上，毕竟前面也说了Nerf是个特殊情况。

损失函数

$\mathcal L=\sum_{\bm p_0,\bm v}\|\bm C(\bm p_0,\bm v)-\bm C^*(\bm p_0,\bm v)\|^2+\lambda\Omega(A(\bm p_0,\bm v))$

其中，$\Omega$表示贝塔分布（BetaDistribution）正则化。

显然，$\|\bm C(\bm p_0,\bm v)-\bm C^*(\bm p_0,\bm v)\|$是输出与Ground truth之间的差；最后加上的$\Omega(A(\bm p_0,\bm v))$是要强迫$A(\bm p_0,\bm v)$降到0，即每个像素的光线上积累的透明度都必须降到0，从而方便优化。

体素裁剪

损失函数已经有了，相比于Nerf的训练，NSVF的训练就多了一个体素裁剪的步骤。

体素裁剪的标准为：

$V_i \text{ is pruned if } \mathop{min}\limits_{j=1\dots G}e^{-\sigma(\tilde{g_i}(\bm p_j))}>\gamma, \bm p_j\in V_i, V_i\in\mathcal{V}$

其中$\{\bm p_j\}^G_{j=1}$表示在体素$V_i$内部均匀采样$G$个点 即：对于体素集$\mathcal{V}$中的某个体素$V_i$，在体素内部均匀采样$G$个点进行推断取得概率密度$\sigma(\tilde{g_i}(\bm p))$，并计算$e^{-\sigma(\tilde{g_i}(\bm p))}$，若所有这些点的计算结果中的最小值大于$\gamma$（即所有点$\bm p$的$\sigma(\tilde{g_i}(\bm p))$中的最大值都不到$-ln(\gamma)$），就裁掉这个体素$V_i$。

训练流程

1. 将空间初始化为边长为$l\approx\sqrt[3]{V/1000}$的1000个体素（即把空间划分成$10\times 10\times 10$个体素）
2. 按照上述损失函数进行训练
3. 按照上述体素裁剪方法进行裁剪
4. 将每个剩余体素再划分为8个（即$2\times 2\times 2$）边长减半的更小体素，小体素多出来的顶点嵌入向量由原有体素的顶点嵌入向量插值而来
5. 回到步骤2，知道达到指定的体素精度

总结

不仅Nerf用体素思想，Neural SDF的加速也用了同样的体素思想

核心思想：

• 传统Nerf/NeuralSDF推断：DNN输入坐标输出颜色密度/SDF值，3D模型信息存储于DNN内部
• 结合体素思想的Nerf/NeuralSDF推断：DNN输入坐标和向量输出颜色密度/SDF值，向量来自于待渲染坐标所在体素的顶点处存储的向量在坐标处的插值，3D模型信息存储于DNN内部和向量中
  • 表示模型信息的向量在不同的论文里叫不同的名字：
    • “feature vector”、“embedding” Neural sparse voxel fields
    • “latent vector” DeepSDF: Learning Continuous Signed Distance Functions for Shape Representation
    • “encoding” Instant neural graphics primitives with a multiresolution hash encoding
• 传统Nerf/NeuralSDF训练：反向传播更新模型参数
• 结合体素思想的Nerf/NeuralSDF训练：反向传播更新模型参数和各体素顶点处存储的向量，并标记空体素
• 传统Nerf/NeuralSDF渲染：ray marching采样生成输入坐标
• 结合体素思想的Nerf/NeuralSDF渲染：ray marching跳过空体素采样生成输入坐标

优势：

• DNN模型可以很小还能保证输出效果，因为大部分模型信息存在表示模型信息的向量里，DNN只需要进行“解码”
• 同样数量的采样点ray marching采样密度可以很高，因为可以跳过空体素，把采样点全放非空体素里
• 训练速度快，因为DNN训练好后对新的3D模型只需要“训练”各体素顶点处存储的向量，这个过程比反向传播训练DNN简单

劣势：

• 初次训练过程复杂：不仅需要改DNN参数，还需要改各体素顶点处存储的向量，还需要判定并标记空体素
• 数据量大：需要在各体素顶点处存储向量，要存储的数据量通常比传统Nerf/NeuralSDF里的DNN模型大很多

针对上述劣势进一步优化: (ACM TC) Instant neural graphics primitives with a multiresolution hash encoding

一种通用的模型输入编码数据结构，实验展示了其可用于图像生成模型、SDF模型、NRC光场模型、Nerf模型的快速训练

相关工作

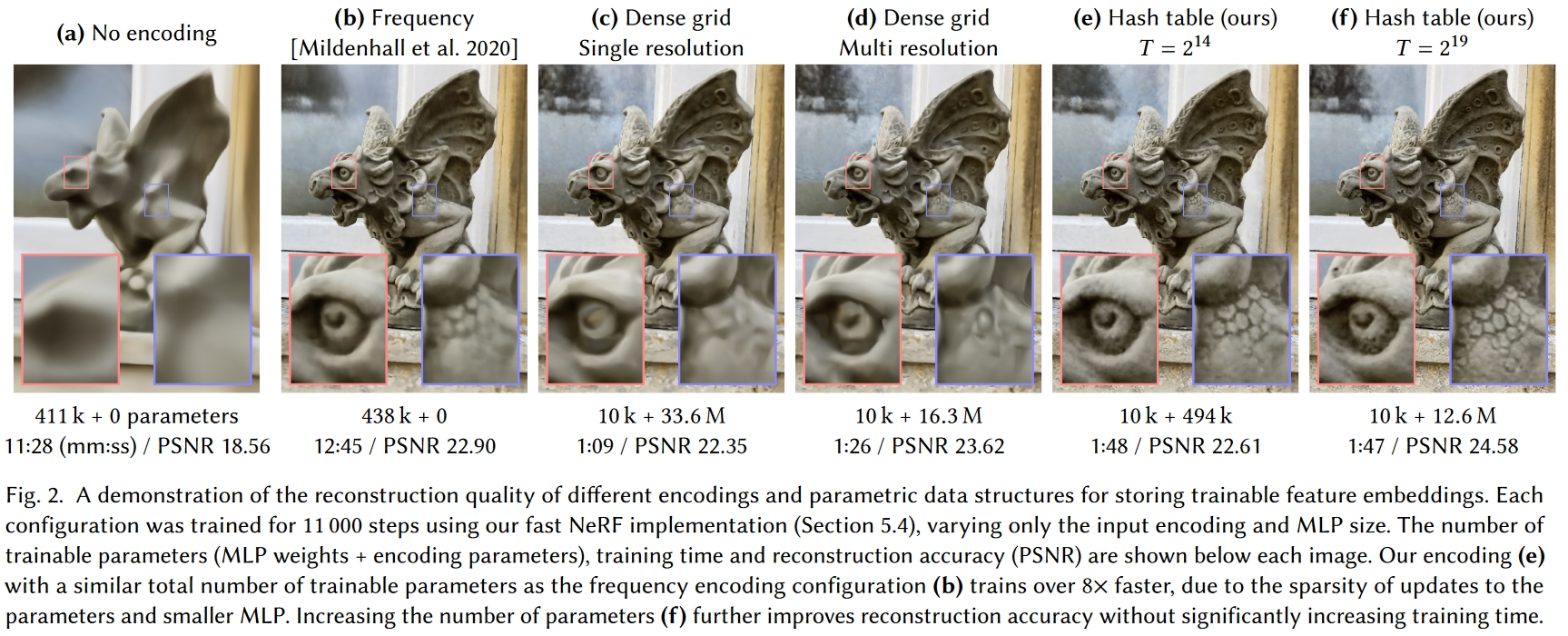
这图直观地展示了在输入中增加信息的重要性：

• 图a纯Nerf很糊，DNN很大
• 图b给输入加上了不可学习的三角函数位置编码（同初代Transformer位置编码），变清晰了一点
• 图c就是NSVF的体素+可学习编码方案，但是没有多尺度体素也没有体素裁剪，可以看到质量差不多的情况下，DNN显著变小，但是要存很大的编码数据，$128^3$个体素里面只有53807个（2.57%）体素有内容
• 图d就是完整的NSVF方案，比图c多了多尺度和体素裁剪，体素分辨率从$16^3$到$173^3$，分辨率大大提升的同时编码数据大大减小了，输出的效果还更精致
• 图e
• 图f

(SIGGRAPH '22) Variable Bitrate Neural Fields

可变码率Nerf