LapSRN

传统的超分辨做法有一些共同之处，首先是L2 loss函数，其次，使用特定尺寸的图片输入（VDSR除外），最后，都是输入到结果，无中间的超分辨率结果

论文先指出了传统SR（super resolution）做法中的一些问题：

1. 现有方法可以处理各个尺寸的低分辨率图片，利用线性插值 将输入图片转为指定尺寸，这一步骤增加了人为噪声
2. 使用L2 loss函数不可避免的产生模糊的预测，因为L2 loss函数不能找到由低分辨率LR到高分辨率HR的潜在的多模态分布，在这里作者做了一个解释：例如，一个低分率的patch可能对应多个高分率的patch，采用L2 loss使得重构结果过度平滑，不符合人类视觉
3. 传统作法无法产生中间的输出结果

于是，针对传统做法的问题，论文做了一些改进

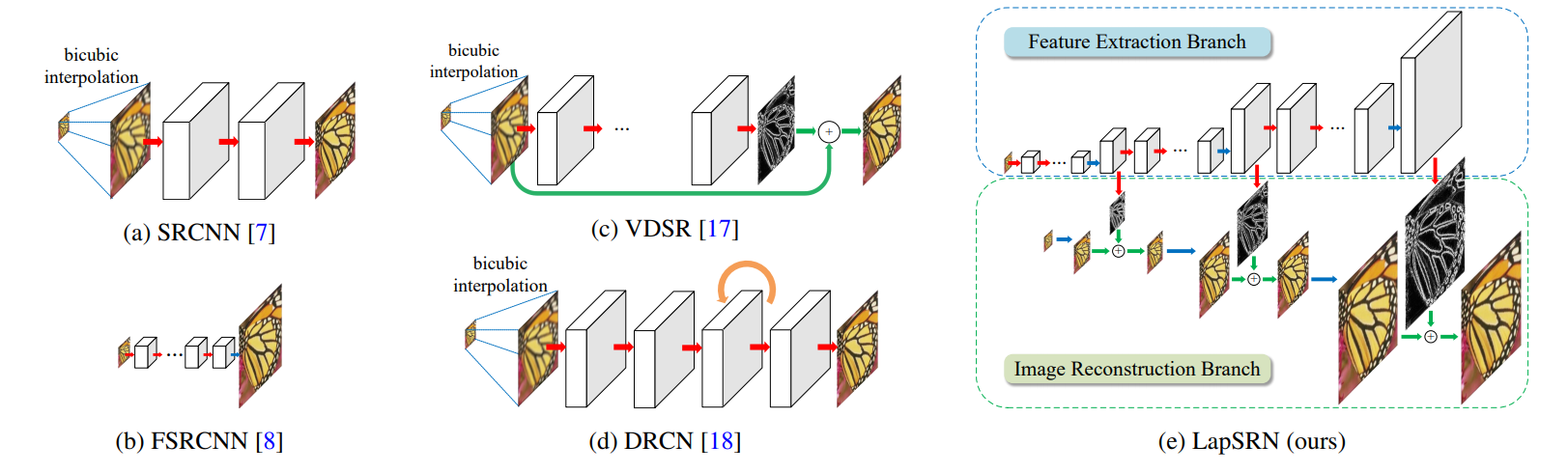
该篇论文的创新点：

1. 级联结构（金字塔结构）：网络有两个分支，1个是特征提取分支，1个是图像重构分支
   • 由图中可见，网络结构为级联结构，个别层有两个箭头输出，向下的箭头表示表示每次上采样到一定程度，即将学习到的残差结果输出，得到对应的重构图像，向右的箭头表示同时继续上采样
   • 与VDSR不同的是，该网络是逐步学习，而不是像其他网络一样只有一个输出，通过级联学习，输出不同scale的残差，得到对应scale的重构结果，一步步得到最终结果
2. 提出一种新的loss函数：
   • $x$表示LR图像，$y$表示HR图像，$r$表示残差，$s$表示对应的level，也就是scale在level $s$下，期望的HR输出为$y_s=x_s+r_s$；$i$是batch中的样本，$N$是每个batch中的图片数量，$L$为金字塔结构的level数量
   • 很明显，这个Loss函数不仅算了最终高清图的Loss，还把中间输出的几个中等清晰度的图片也拿去算了Loss

$\begin{aligned} \mathcal L(\hat y,y;\theta)&=\frac{1}{N}\sum_{i=1}^N\sum_{s=1}^L\rho\left(\hat y^{(i)}_s-y^{(i)}_s\right)\\ &=\frac{1}{N}\sum_{i=1}^N\sum_{s=1}^L\rho\left((\hat y^{(i)}_s-x^{(i)}_s)-r^{(i)}_s\right) \end{aligned}$